[algorithm] dynamic programming [python]

복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법이다. 1 부분 문제 반복(Overlapping subproblems)과 최적 부분 구조(Optimal substructure)를 가지고 있는 알고리즘을 일반적인 방법에 비해 더욱 적은 시간 내에 풀 때 사용한다.\
여기서 부분 문제 반복과 최적 부분 구조를 가지고 있다에서
부분 문제의 해는 전체 문제의 해를 구할 때 필요해야한다.

Tabulation

하향식 Bottom-Up 방식이라고도 한다.
최초 값부터 차례대로 계산해 나가는 방식이다

def fibonacci_dp(num):
    f = [0, 1]
    for i in range(2, num+1):
        f.append(f[i-1] + f[i-2])
    return f

Memoization

<동일 계산 반복시>
이전 계산값을 메모리에 저장하여(메모리 공간을 약간 더 사용한다)(캐싱이라고도 한다.)
매번 다시 실행하지 않도록해서 / 실행 속도를 빠르게 하는 기술이다.

상향식 Top Down 방식이라고도 한다.

def fibonacci_memoi(num):
    global memo
    if num >= 2 and len(memo) <= num:
        memo.append(fibonacci_memoi(num-1) + fibonacci_memoi(num-2))
    return memo[num]
memo = [0, 1]

or

dp = [0]*100 # 소문제 결과를 저장할 리스트
dp[0] = 1 
dp[1] = 1

def fib(n):
    
    # 만약 계산한 적이 없다면 재귀로 계산 
    if dp[n] == 0:
        dp[n] = fib(n-1) + fib(n-2)
    
    # 있다면 그대로 반환 
    return dp[n]

fib(10)

examples

스트링편집거리 - tabulation bottom-top

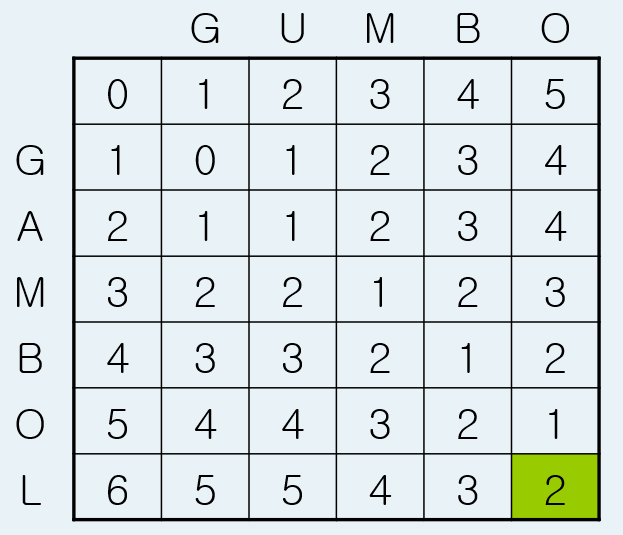
def edit_distance(s:str, t: str):
    m = len(s)+1
    n = len(t)+1
    D = [[0]*m for _ in range(n)]
    D[0][0] = 0
    
    for i in range(1,m):
        D[0][i] = D[0][i-1] + 1
    
    for j in range(1,n):
        D[j][0] = D[j-1][0] + 1
    
    for i in range(1,n):
        for j in range(1,m):
            cost = 0

            if s[j-1] != t[i-1]:
                cost = 1
            
            D[i][j] = min(D[i][j-1] + 1,D[i-1][j] + 1, D[i-1][j-1] + cost)
    
    return D[n-1][m-1]
                
edit_distance('GUMBO', 'GAMBOL')